Discrete event simulation (DES) is a methodology for modelling dynamic systems as a sequence of events in time. There are plenty of places to read about DES, but in this note I want to outline how it works and can be simply implement, recognising several subtleties. DES is widely used in different areas where analytical solutions are difficult; I am focusing on its use in modelling digital logic and computer systems.

In a DES, each event is scheduled to occur at a particular point in time and represents a change in the state of the system and the possible generation of future events. Because there are no state changes between events, the simulation jumps through time from one event to the next. These variable time steps are in contrast with a discrete-event scheme with fixed timesteps. Fixed timesteps are particularly suited to digital systems with clocked logic, where each time increment corresponds to clock cycle. Fixed-time simulation has the drawback that all time steps are evaluated regardless of whether anything happens, although it is easier to reason about since everything proceeds in lockstep. DES is inherently more flexible but can be harder to parallelise because of the need to maintain a centralised event list.

Operation

The main components of a DES are:

  • A state (or set of states) representing the components of the system.
  • Events, that occur atomically at a particular instant and can update the system state and create new future events.
  • A clock, that records the simulation time.
  • A list of future events (the event list). This is most often implemented as a priority queue with events queued in chronological order, soonest at the front.

An outline of the DES algorithm is as follows:

  • Create one or more initial events and add them to the event list.
  • While the event list not empty:
    • Choose a next event with the earliest time.
    • Advance simulation clock to time of event.
    • Execute the event.
      • State updates are committed immediately.
      • New events are added to the event queue.

Simulation proceeds until there are no more events to process, or a maximum time is reached.

During the simulation the following must be ensured:

  1. For events that occur at the same time, it must be possible to execute them in any order, without affecting the behaviour of the simulation. In other words, the outcome of the simulation must not depend on any ordering of simultaneous events.

  2. Duplicate events must not be created. For example, if a component of the system is servicing some kind of input queue, when an item is added to the queue a corresponding ‘service’ event must be created, but only when the queue is empty. As such, delegation of responsibility for event creation must be clear.

To avoid violating point 1 above, each time step can be divided into phases to impose an ordering of events.

The simplest case is to divide each timestep into two phases to serialise the handling of two dependent events. As an example, consider nodes in a ring topology that can pass tokens between themselves in one direction, with it taking one timestep to for a token to traverse one node. Each node has two associated events: transmit and receive. It must hold that a transmit event for a node must be scheduled any receive events for that node have been processed. By separating event processing in this way, there can be no dependencies between the serialisation of transmit and receive events as they are fetched from the simulation queue.

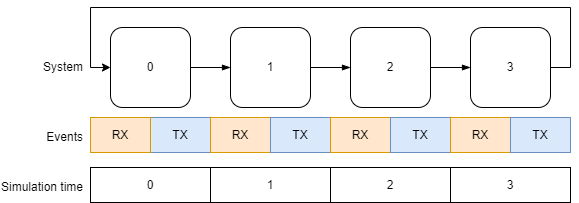
DES of a ring of nodes that exchange a token with events for transmit and receive, separated by different phases within a simulation timestep.
DES of a ring of nodes that exchange a token with events for transmit and receive, separated by different phases within a simulation timestep.

Extending this concept of phases, a timestep can be divided into an arbitrary number of sub phases to model more complex behaviours. An interesting example of this is SystemVerliog, which defines its execution semantics in terms of multi-phase discrete event simulation. Roughly, a design or test bench defines a set of stateful processes that respond to changes on their inputs to produce outputs. Every change in state of a net or variable causes processes sensitive to them to be evaluated. There may be many steps of evaluation to produce a final output for the timestep. The timestep is divided into a fixed set of ordered regions (17 in total) to provide predictable interactions with a design. Within a region, many events may be processed and further ones scheduled to resolve sensitivity dependencies.

Example implementation

Using the above example of a ring of nodes passing a token around them, the following Rust code implements a DES of the system. This is a very simple DES example and only one possible implementation, but sufficient to illustrate the main concepts.

The main component is a Simulator object that maintains the event queue and the system state:

struct Simulator {
    max_cycles: usize,
    current_time: usize,
    event_queue: BinaryHeap<Event>,
    state: State,
}

Events have a type, a time at which they occur and node in the system that they belong to. The node_id is used for directing state updates.

#[derive(Debug, PartialEq, Eq, PartialOrd, Ord)]
enum EventType {Transmit, Receive }

#[derive(Debug, PartialEq, Eq, PartialOrd, Ord)]
struct Event {
    event_type: EventType,
    time: usize,
    node_id: usize,
}

The main simulation loop pops events off of the queue while it is not empty and dispatches them to a handler function:

fn run(&mut self) {
        while let Some(event) = self.event_queue.pop() {
            if self.max_cycles > 0 && self.current_time >= self.max_cycles {
                break;
            }
            self.current_time = event.time;
            self.handle_event(event);
        }
    }

The simulation current_time is updated to the time of the current event being processed. The event handler function implements the behaviour for each event:

fn handle_event(&mut self, event: Event) {
        match event.event_type {
            EventType::Transmit => {
                // Deactivate.
                self.state.nodes[event.node_id].active = false;
                println!("Node {} inactive", event.node_id);
                // Schedule receive at next node.
                let recv_event = Event {
                    event_type: EventType::Receive,
                    time: self.current_time + 1,
                    node_id: self.state.next_node(event.node_id),
                };
                self.schedule_event(recv_event);
            }
            EventType::Receive => {
                // Activate.
                self.state.nodes[event.node_id].active = true;
                println!("Node {} active", event.node_id);
                // Schedule transmit.
                let send_event = Event {
                    event_type: EventType::Transmit,
                    time: self.next_timestep(self.current_time),
                    node_id: event.node_id,
                };
                self.schedule_event(send_event);
            }
        }
    }

Each event action updates the node state and creates a new event corresponding to the passing of the token to the next node of the ring.

The simulation is setup with a initial receive event at node 0:

let mut sim = Simulator::new(20);
for _ in 0..10 {
    sim.state.add_node();
}
let initial_event = Event { event_type: EventType::Receive, time: 0, node_id: 0 };
sim.schedule_event(initial_event);
sim.run();

And running it produces the output:

Node 0 active
Node 0 inactive
Node 1 active
Node 1 inactive
Node 2 active
Node 2 inactive
Node 3 active
Node 3 inactive
Node 4 active
Node 4 inactive
Node 5 active
Node 5 inactive
Node 6 active
Node 6 inactive
Node 7 active
Node 7 inactive
Node 8 active
Node 8 inactive
Node 9 active
Node 9 inactive

The complete source code for the example can be found in this Gist.

There are many libraries for implementing DES such as SystemC and SimPy. Different libraries provide varying approaches for creating and managing events with supporting infrastructure, and their applicability depends on the application and system being simulated.

Summary

This note explains how DES simulation works and how it simple to implement. DES is well suited to modelling synchronous and asynchronous digital systems, but care must be taken to ensure that simultaneous events are scheduled without dependencies and events are not duplicated.

References / further reading